如何直观的解释梯度下降算法？

1 引言

根据前面的介绍可以知道，梯度下降算法的目的是用来最小化目标函数，也就是一个求解的工具。当目标函数取到（或接近）全局最小值时，我们也就求解得到了模型所对应的参数。不过那什么又是梯度下降（Gradient Descent）呢？如图1所示，假设有一个山谷，并且你此时处于位置$A$处，那么请问以什么样的方向（角度）往前跳，你才能最快的到达谷底$B$处呢?

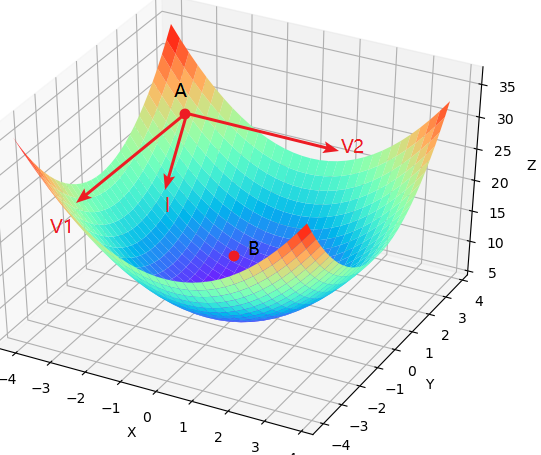
现在你大致有三个方向可以选择，沿着X轴的$\overrightarrow{V1}$方向，沿着Y轴的$\overrightarrow{V2}$方向以及沿着两者间的$\overrightarrow{l}$方向。其实不用问，大家都会选择$\overrightarrow{l}$所在的方向往前跳第一步，然后接着再选类似的方向往前跳第二步直到谷底。可为什么都会这样选呢？答：这还用问一看就知，不信你自己看。

2 梯度下降算法

2.1 方向导数与梯度

在学习一元函数导数时我们知道，$f(x)$在$x_0$处的导数反映的是$f(x)$在$x=x_0$处时的变化率；$|f^{\prime}(x_0)|$越大，也就意味着$f(x)$在该处的变化率越大，即移动$\Delta x$后产生的函数增量$\Delta y$越大。同理，在二元函数$z=f(x,y)$中，为了寻找$z$在$A$处的最大变化率，就应该计算函数$z$在该点的方向导数

其中$\overrightarrow{l}$为单位向量，$\alpha,\beta$分别为$\overrightarrow{l}$与$x$和$y$轴的夹角，$\theta$为梯度方向与$\overrightarrow{l}$的夹角。

根据式$(1)$可知，要想方向导数取得最大值，那么$\theta$必须为$0$。由此可知，只有当某点处方向导数的方向与梯度的方向一致时，方向导数在该点才会取得最大的变化率。

在图1中，已知$z=x^2+y^2+5$，$A$的坐标为$(-3,3,23)$，则$\partial z/\partial x=2x,\partial z/\partial y=2y$。由此可知，此时梯度在点$A$处的方向为$(-6,6)$。所以，当你站在在$A$点沿各个方向往前跳同样大小的距离时，只有沿着$(\sqrt{2}/2,-\sqrt{2}/2)$这个方向（进行了单位化，且同时取了相反方向，因为这里要的是负增量）才会产生最大的函数增量$\Delta z$。

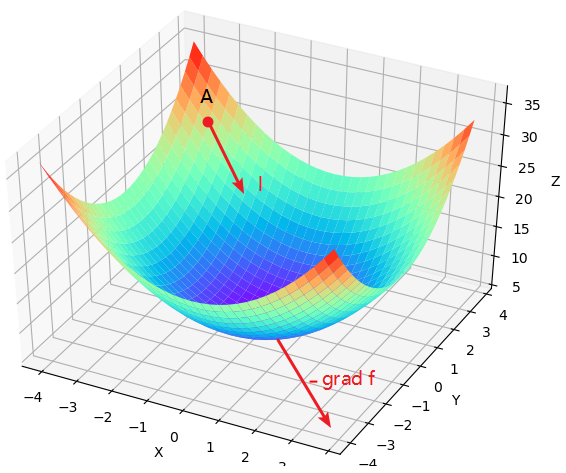
如图2所示，要想每次都能以最快的速度下降，那么每次都必须向着梯度的反方向向前跳。

2.2 梯度下降

介绍这么多总算是把梯度这回事儿给说清楚了，那么如何用具体的数学表达式进行描述呢？总不能一个劲儿的喊它“跳”对吧。为了方便后面的表述以及将读者带入到一个真实求解的过程中，这里先将图1中的字母替换成模型中的参数表述。

现在有一个模型的目标函数$J(w_1,w_2)=w_1^2+w_2^2+2w_2+5$（为了方便下面可视化此处省略了参数$b$，但是原理都一样），其中$w_1,w_2$为待求解的权重参数，且随机初始化点$A$为初始权重值。下面就一步步的通过梯度下降法来进行求解。

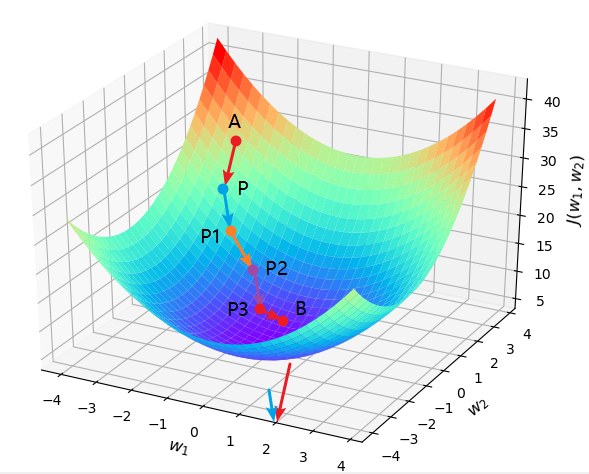
如图3所示，设初始点$A=(w_1,w_2)=(-2,3)$，则$J(-2,3)=24$，且点$A$第一次往前跳的方向为$-grad\ J=-(2{{w}_{1}},2{{w}_{2}}+2)=(1,-2)$。

如图4所示，$\bf{OQ}$为平面上梯度的反方向，$\bf{AP}$为其平移后的方向，但是长度为之前的$\alpha$倍。因此，根据梯度下降的原则，此时曲面上的$A$点就该沿着其梯度的反方向跳跃，而投影到平面则为$A$应该该沿着$\bf{AP}$的方向移动。假定曲面上$A$点跳跃到了$P$点，那么对应在投影平面上就是图4中的$\bf{AP}$部分，同时权重参数也从$A$的位置更新到了$P$点的位置。

从图4可以看出，向量$\bf{AP},\bf{OA},\bf{OP}$三者的关系为

进一步，可以将式$(2)$改写成

又由于$\bf{OP},\bf{OA}$本质上就是权重参数$w_1,w_2$更新后与跟新前的值，所以便可以得出梯度下降的更新公式

其中$W=(w_1,w_2)$，$\partial J/\partial W$为权重的梯度方向，$\alpha$为步长，用来放缩每次向前跳跃的距离。同时，将式代入具体数值后可以得出，曲面上的点$A$在第一次跳跃后的着落点为

此时，权重参数便从$(-2,3)$更新到了$(-1.6,2.2)$。当然其目标函数$J(w_1,w_2)$也从$24$更新到了$16.8$。至此，我们便详细的完成了一轮梯度下降的计算。当$A$跳跃到$P$之后，又可以再次利用梯度下降算法进行跳跃，直到跳到谷底（或附近），如图5所示。

2.3 代码示例

最后，根据上述原理，还可以通过实际的代码将整个过程展示出来：

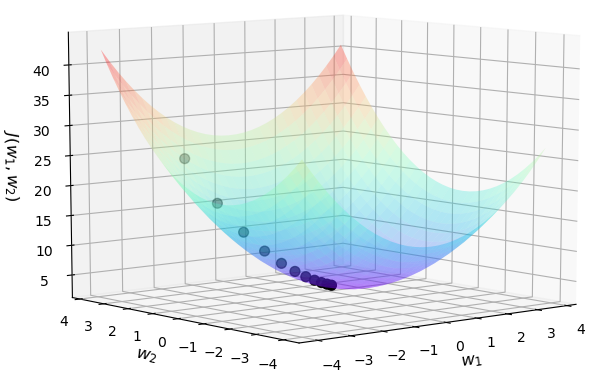
xxxxxxxxxx
27
1
def cost_function(w1, w2):
2
    J = w1 ** 2 + w2 ** 2 + 2 * w2 + 5
3
    return J
4
def compute_gradient(w1, w2):
5
    return [2 * w1, 2 * w2 + 2]
6
​
7
def gradient_descent():
8
    w1, w2 = -2, 3
9
    jump_points = [[w1, w2]]
10
    costs = [cost_function(w1, w2)]
11
    step = 0.1
12
    print("P:({},{})".format(w1, w2), end=' ')
13
    for i in range(20):
14
        gradients = compute_gradient(w1, w2)
15
        w1 = w1 - step * gradients[0]
16
        w2 = w2 - step * gradients[1]
17
        jump_points.append([w1, w2])
18
        costs.append(cost_function(w1, w2))
19
        print("P{}:({},{})".format(i + 1, round(w1, 3), round(w2, 3)), end=' ')
20
    return jump_points, costs
21
​
22
if __name__ == '__main__':
23
    jump_points, costs = gradient_descent()
24
    plot_surface_and_jump_points(jump_points, costs)
25
    
26
# 部分结果：P:(-2,3) P1:(-1.6,2.2) P2:(-1.28,1.56).....P20:(-0.023,-0.954)

通过上述Python代码便可以详细展示跳向谷底时每一次的落脚点，并且可以看到谷底的位置就在$(-0.023,-0.954)$附近，如图6所示。此致，就介绍完了如何通过编码来实现梯度下降算法的求解过程，等后续完成线性回归模型的推导后，再来自己编码完成线性回归模型的参数求解过程。

3 小结

在本节中，笔者通过一个跳跃的例子详细给大家介绍了什么是梯度，以及为什么要沿着梯度的反方向进行跳跃；然后通过图示导出了梯度下降的更新公式

在这里笔者又写了一遍是希望大家脑子里一定要记住这个公式，以及它的由来。因为它同时也是求解神经网络的主要工具，也是目前的唯一工具。同时，可以看出，通过梯度下降算法来求解模型参数需要完成的一个核心就是计算参数的梯度。最后，虽然公式介绍完了，但值得注意的是公式中的步长$\alpha$也是一个十分重要的参数。