1 引言
在上一篇文章中,笔者分别就SVM中软间隔与硬间隔目标函数的求解过程进行了介绍。但是在实际应用过程中,从效率的角度来讲那样的做法显然是不可取的,尤其是在大规模数据样本和稀疏数据中[1]。在接下来的这节内容中,笔者将会介绍一种新的求解算法,序列最小化优化算法来解决这一问题。
2 SVM软间隔求解
序列最小优化算法(Sequential Minimal Optimization, SMO)于1998年由John Platt所提出,并且SMO算法初次提出的目的就是为了解决SVM的优化问题[2]。SMO算法是一种启发式的算法,它在求解过程中通过以分析的方式来定位最优解可能存在的位置,从而避免了传统方法在求解中所遭遇的大量数值计算问题,并且最终以迭代的方式来求得最优解。在正式介绍SMO算法之前,笔者将先来介绍SMO算法的基本原理坐标上升算法(Coordinate Ascent)。
2.1 坐标上升算法
在之前的文章中,笔者详细的介绍了什么是梯度下降算法以及梯度下降算法的作用。对于一个待优化的目标函数来说,在初始化一个起始位置后,便可以以该点为基础每次沿着该点梯度的反方向向前移动一小步,以此来迭代求解得到目标函数的全局(局部)最优解。而所谓的坐标上升(下降)算法可以看作是初始位置只沿着其中的一个(或几个)方向移动来求解得到目标函数的全局(局部)最优解[3],如图1所示。
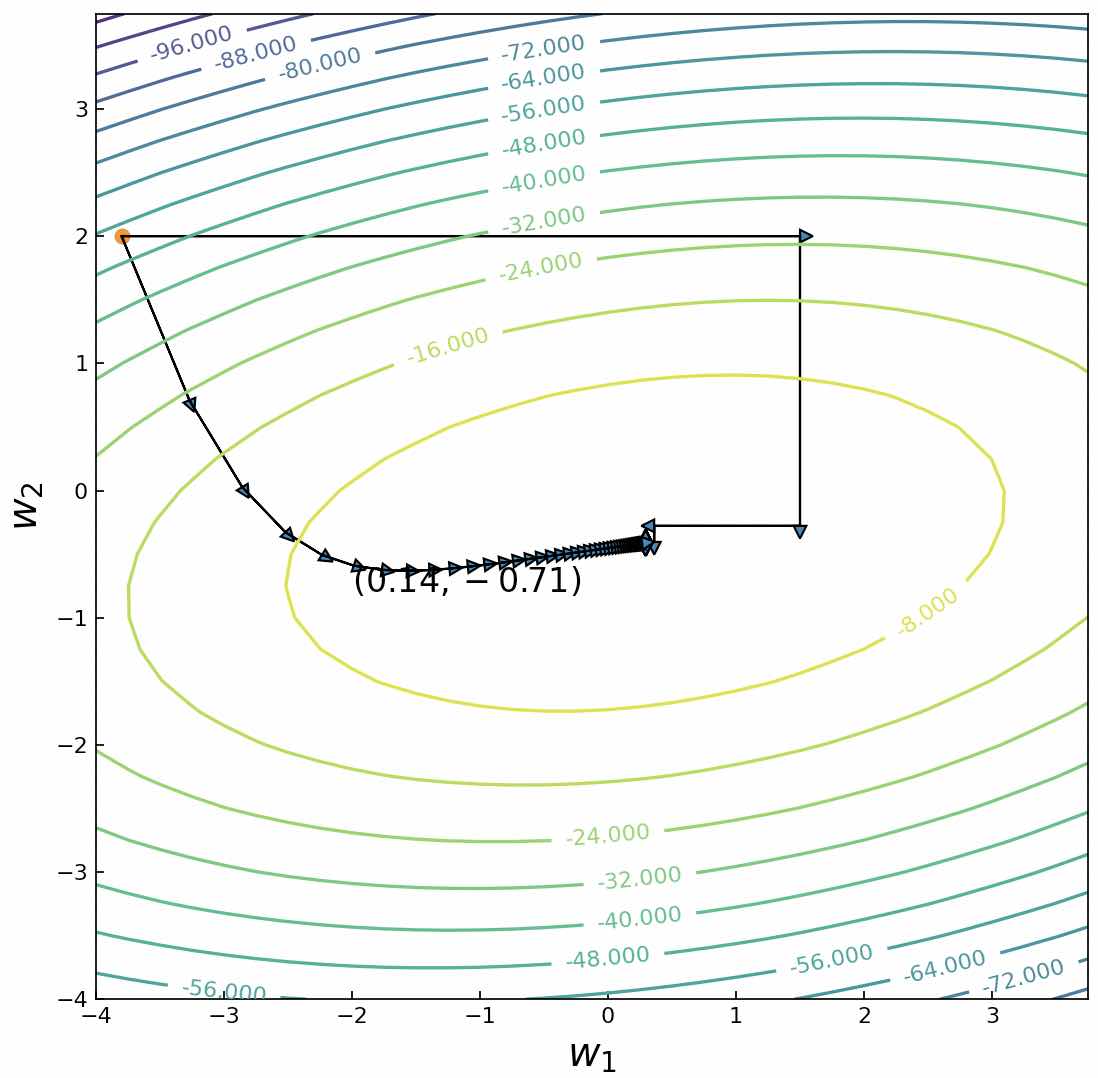
在图1中,彩色曲线为目标函数的等高线,黑色箭头曲线为梯度上升算法最大化目标函数的求解过程,而黑色箭头折线为坐标上升算法最大化目标函数的求解过程。 具体的,对于待求解目标函数来说可以通过如下步骤来进行求解
(1) 随机初始化向量为初始参数值;
(2) 在中依次选择为变量固定其它参数为常量,然后求目标函数关于的导数并令其为0求得;
(3) 重复执行步骤(2)直到目标函数收敛或者是误差小于某一阈值结束。
例如在上面这个示例中的求解表达式分别为
那么在初始化一组后,便可以通过式来迭代求解得到的解。
同时,上述步骤(2)对于顺序的选择这里采用了最为简单的按顺序依次进行,一种更优的做法便是每次选择余下常量中能够使得目标函数产生最大增量参数作为优化对象。
2.2 SMO算法思想
根据之前的内容可知,SVM软间隔最终需要求解的目标函数为
假设随机初始化后的均满足式中的约束条件,现在通过坐标上升算法来求解。如果此时固定为常量,为变量来求解,那么这样能够求解得到吗?答案是不能[[4]。因为根据式中第2个约束条件有
进一步,在式两边同时乘上有
根据式可知,完全取决于,如果固定那么也就意味着也是固定的。因此,在这样的情况下每次至少需要同时选择两个参数为变量,同时再固定住其它变量才能够最终求得所有参数。
此时,假设固定不变来求解参数。根据式中的约束条件有
由于此时式右边是固定的,因此可以用一个常数来表示
进一步,可以将表示为
此时,式中的目标函数便可以改写为
在式中,由于此时固定为常数,因此其可以简单表示为一个关于的一元二次多项式。
接着,对于式来说通过令的导数为0便可以轻易求得的取值;然后再将代入式即可得到的值。进一步,按照相同的过程便可求得的值,最后再重复执行上述整个过程便可以迭代求解得到。
以上就是SMO算法求解的主要思想。虽然看起来不太复杂,但是里面仍旧有很多值得深究的内容,下面开始正式介绍SMO算法的原理。
2.3 SMO算法原理
为了更加广义的表示SVM软间隔中的优化问题,可以通过如下形式来表示待求解的优化问题
其中为任意核函数。
进一步,不失一般性,这里假设首先选择参数为变量,固定其它参数为常量。于是式便可以改写成如下形式[1]
其中,表示与无关的常量。
同时,记
则目标函数可以改写为
将代入式便可以得到一个只含有变量目标函数
进一步式关于的导数为
令式为0可以得到
此时,记
那么在初始化一组后,将式和代入式有
将式进一步化简后可得
到此,便初步求得了的求解表达式。为什么是初步呢?因为此时的求得的还没有经过约束条件裁剪。
由式中的第1个约束条件可知,的解只能位于这个正方形盒子中;进一步,由式中的第2个约束条件可知,还必须位于平行于盒子对角线的线段上,如图2所示。
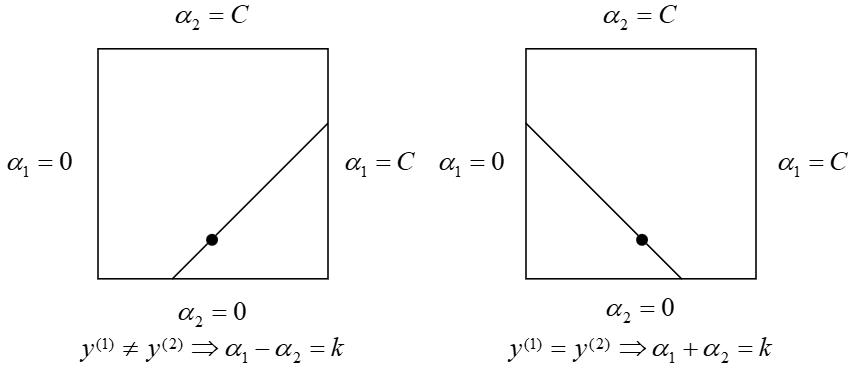
图 2. 约束条件下的修正图
如图2所示,的解只能位于盒子内部的线段上。由式可知根据式求得到的值必定位于线段所在的直线上,因此还需要使得满足
其中,与是图2中线段的两个端点。
从图2可以看出,如果则
如果则
因此,裁剪后的值应该为
进一步,由和可得
到此就介绍完了的求解步骤。进一步,可以按照类似的方法求解得到;最后再迭代整个过程便可以求解得到的最优解。
2.4 偏置求解
在每次计算得到两个变量后,都需要同步的来更新偏置的值。
例如当求得时,根据式中的第3个KKT条件可知
进一步可得
于是根据式有
由式中的定义可知
根据式可知,式的前两项可以改写为
最后,将式代入式可得
同理可得,当时有
同时,当同时满足条件时,那么均是有效的,且两者相等。如果为或者,那么所有在之间的值均满足KKT条件的值,此时选择两者的均值作为,即
2.5 SVM算法求解示例
经过前面几部分内容的介绍,相信各位读者朋友对于如何通过SMO算法来求解SVM中的参数已经有了一定的了解。同时,对于整个求解过程还可以通过如下一段伪代码来进行表示[5]
输入:
xxxxxxxxxx71$C$惩罚项系数;23$tol$:误差容忍度;45$max\_passes$:当$\alpha_i$不再发生变化时继续迭代更新的最大次数;67$(({{x}^{(1)}},{{y}^{(1)}}),...,({{x}^{(m)}},{{y}^{(m)}}))$:训练集;
输出:
xxxxxxxxxx31$\alpha\in\mathbb{R}^m$:求解得到的拉格朗日乘子;23$b\in\mathbb{R}$:求解得到的偏置。
xxxxxxxxxx251初始化所有 alpha_i = 0, b = 0, passes = 02while (passes < max_passes)3 num_changed_alphas = 04 for i = 1,...,m5 计算 E_i6 if ((y_i*E_i < -tol and a_i < C)||(y_i*E_i > tol and alpha_i > 0))7 随机选择j,且j不等于i8 计算 E_j9 保存:alpha_i_old = alpha_i,alpha_j_old = alpha_j10 计算 L 和 H11 if (L == H):12 continue13 计算 eta14 if (eta >- 0):15 continue16 计算 alpha_j并裁剪17 if (|alpha_j - alpha_j_old| < 10e-5):18 continue19 分别计算alpha_i, b_1, b_220 计算b21 num_changed_alphas += 122 if (num_changed_alphas == 0):23 passes += 124 else:25 passes = 0当然,根据上述伪代码的描述,还可以通过代码将其完整的实现,具体可以参见[6]。同时,根据实现的代码,如果以图3里的数据样本为输入,且惩罚系设为 ,那么最终的求解结果为
xxxxxxxxxx71data_x = np.array([[5, 1], [0, 2], [1, 5], [3., 2], [1, 2], [3, 5], [1.5, 6], [4.5, 6], [0, 7]])2data_y = np.array([1, 1, 1, 1, 1, -1, -1, -1, -1])3alphas, b = smo(C=.2, tol=0.001, max_passes=200, data_x=data_x, data_y=data_y)4print(alphas) #[0. 0. 0.2 0.142 0. 0.2 0.142 0. 0.]5print(b)# 2.666w = compute_w(data_x,data_y,alphas)7print(w)# [-0.186, -0.569]
根据上述输出结果可知,,即对应的支持向量为 ,,且同时,。需要注意的是,为了作图方便,图3中左右两边各自还有两个样本点没有画出,所以上述代码中有9个样本。
3 总结
在本节中,笔者首先以坐标上升算法为铺垫,介绍了SMO算法的基本思想,从整体层面上阐述了SMO算法的求解过程;然后详细介绍SMO算法的具体求解过程及原理,包括参数偏置的求解方法;最后以伪代码的形式展示了SMO算法的求解过程,并通过一个实例进行了展示。
本次内容就到此结束,感谢您的阅读!如果你觉得上述内容对你有所帮助,欢迎分享至一位你的朋友!若有任何疑问与建议,请添加笔者微信'nulls8'或加群进行交流。青山不改,绿水长流,我们月来客栈见!
引用
[1] John C. Platt. Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines, Microsoft Research Technical Report MSR-TR-98-14.
[2] https://en.wikipedia.org/wiki/Sequential_minimal_optimization
[3] https://en.wikipedia.org/wiki/Coordinate_descent
[4] Andrew Ng, Machine Learning, Stanford University, CS229, Spring 2019.
[5] Machine Learning, Stanford University, CS229, Autumn 2009.


