各位朋友大家好,欢迎来到月来客栈,我是掌柜空字符。
4.1基本概念4.1.1机器学习4.1.2有监督学习4.1.3无监督学习4.1.4小结4.2特征标准化4.2.1等高线4.2.2梯度与等高线4.2.3标准化方法4.2.4 特征组合与映射4.2.5 小结4.3 过拟合4.3.1 模型拟合4.3.2 过拟合与欠拟合4.3.3 解决欠拟合与过拟合4.3.4小结4.4 正则化4.4.1 测试集导致糟糕的泛化误差4.4.2 训练集导致糟糕的泛化误差4.4.3 正则化中的参数更新4.4.4 正则化示例代码4.4.5 小结4.5 偏差方差与交叉验证4.5.1 偏差与方差定义4.5.2 模型的偏差与方差4.5.3 超参数选择4.5.4 模型选择4.5.5 小结4.6 实例分析手写体识别4.6.1 数据预处理4.6.2 模型选择4.6.3 模型测试4.6.4 小结引用推荐阅读
经过前面两章内容的学习,我们已经完成了对线性回归和逻辑回归核心内容的学习,但是一些涉及到模型改善(Optimization)与泛化(Generalization)的内容并没有进行介绍。在第4章中,笔者将以线性回归和逻辑回归为例(同样可以运通到后续介绍的其他算法模型),介绍一些机器学习中常用的模型和数据处理的技巧,以及尽可能的说清楚为什么要这么做的原因。由于这部分的内容略微有点杂乱,所以笔者将按照如图4-1所示的顺序来递进地进行介绍,同时再辅以示例进行说明。不过在正式开始继续介绍后续内容之前,我们先来看看机器学习中的几个基本概念。
以下所有完整实现代码(包括作图)均可从仓库 https://github.com/moon-hotel/MachineLearningWithMe 中获取!公众号后台回复“跟我一起机器学习”即可获得本文高清PDF内容与教学PPT!
4.1基本概念
在经过前面两章内容的介绍后,相信读者朋友们对于机器学习这个概念已经有了一定感官上的认识。不过那到底什么是机器学习呢?
4.1.1机器学习
关于到底什么是机器学习(Machine Learning),可能不同的人有不同的理解,自然也就产生了不同的定义。下面笔者主要介绍一下计算领域内两位大师对于什么是机器学习所给出的定义。
第一位是人工智能先驱亚瑟·塞缪尔(Arthur Samuel),他在1959年创造了“机器学习”一词[1]。塞缪尔认为,所谓机器学习是指:计算机能够具备根据现有数据构建一套不需要进行显示编程的算法模型来对新数据进行预测的能力。这里所谓不需要进行显示编程是区别于传统程序算法需要人为指定程序的执行过程。
第二位是卡内基梅隆大学的计算机科学家汤姆·迈克尔·米切尔(Tom Michael Mitchell),他给出了一个相较于塞缪尔更加正式与学术的定义。米切尔认为,如果计算机程序能够在任务T中学得经验E并且通过指标P来进行评价,同时根据经验E还能够提升程序在任务T的评价指标P,那么这就是机器学习[2]。这段话对于初学者来说稍微有点拗口,其实际想要表达的就是,如果一个计算机程序能够自己根据数据样本学习获得经验并逐步提高最终的表现结果,那这个过程就被称为是机器学习。
可以看出,两位大师虽然在对机器学习进行定义时用了不同的语言来进行描述,但是从本质上来讲他们说的都是一回事,即能让计算机根据现有的数据样本自己“学”出一套规则来的过程。
4.1.2有监督学习
有监督学习(Supervised Learning)也叫做有指导学习,它是指模型在训练过程中需要通过真实值来对训练过程进行指导的学习过程。在有监督模型的训练过程中,每次输入模型的都是形如 这样的样本对,而模型最终学到的就是从输入到输出这样的映射关系。例如在前面两章中介绍的线性回归和逻辑回归,以及后面会陆续介绍到的K近邻、朴素贝叶斯、决策树和支持向量机等都是典型的有监督学习模型,因为这些模型在训练过程中都需要通过真实值来指导模型进行学习。
4.1.3无监督学习
无监督学习(Unsupervised Learning)也叫做无指导学习,它是指模型在训练过程中不需要通过真实值来对训练过程进行指导的学习过程。在无监督模型的训练过程中,模型仅仅只需要输入特征变量便可以进行学习,而模型最终学到的就是输入特征中所潜在的某种模式(Pattern)。例如在第10章中将要介绍的聚类算法就是一类典型的无监督学习模型。
4.1.4小结
在本节中,笔者首先介绍了什么是机器学习这一基本概念,并引述了计算机领域中两位大师分别对机器学习一词的定义;然后介绍了机器学习算法中的两个基本分类,即有监督学习和无监督学习,并同时介绍了两者之间的区别。在介绍完这几个基本概念后,下面将正式开始介绍模型改善与泛化的常用方法。
4.2特征标准化
什么是特征标准化(Standardization)呢?为什么需要特征进行标准化?在回答这两个疑问之前,笔者先来介绍一下什么是等高线。
4.2.1等高线
如图4-2所示,上面部分为的函数图像,而下面部分则为函数的等高线。也就是说,其实等高线就是函数向下的垂直投影。而所谓等高指的就是投影中任意一个环所代表的函数值均相等。反映在3D图形上就是,在曲面上总能找到一个闭环,使得环上每一点的函数值都相等,即距离谷底的高度都相同。
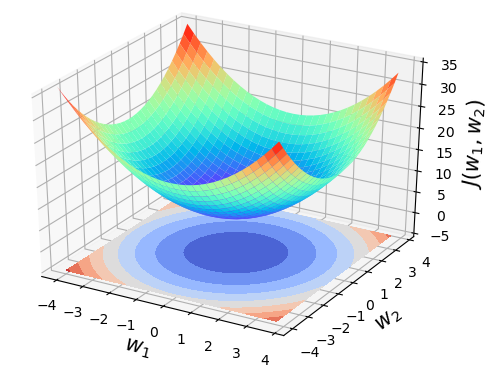
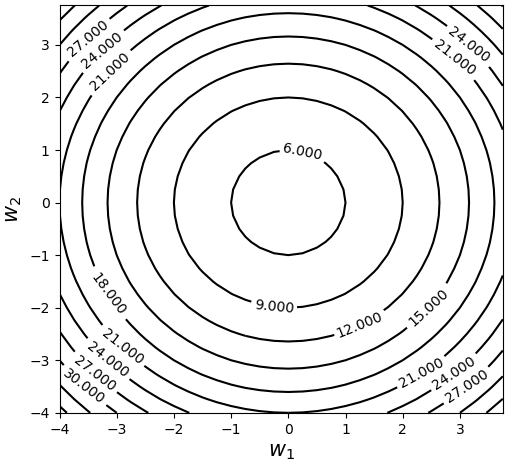
如图4-3所示,同样为函数的等高线图,只不过这次将它展示在了二维平面。在图4-3中,任意一个环代表的都是不同 取值下相等的函数值,同时可以看到中心点为对应的函数值为5,通常这也是通过梯度下降进行求解的最优点。
4.2.2梯度与等高线
由于梯度的方向始终与等高线保持垂直,所以理想情况下不管随机初始点选在何处,我们都希望梯度下降算法能沿着类似如图4-4左边所示的方式达到最低点,而非右边的情形。
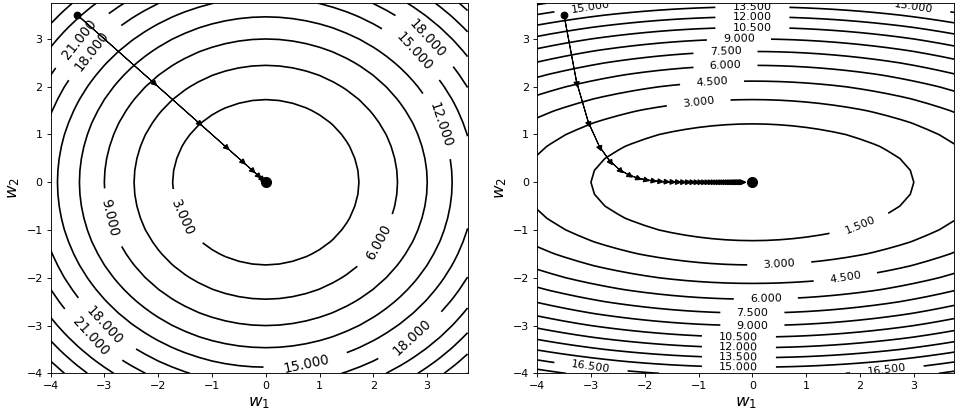
可以看出,若是同时使用梯度下降算法来优化图4-4左右两边所代表的目标函数,那么显然在左边的情形下能够以更快的速度收敛得到最优解。同时,从右图可以看出,若和分别增加相同若干个单位,则增加所带来的函数增量要远大于。例如,当初始点时,从0变化至3的函数增量要远远小于从0变化至3的函数增量,前者约等于1.5左右,而后者约等于12左右。那什么样的目标函数,会使得等高线呈现出椭圆形的环状现象呢?答案就是,若不同特征维度之间的范围差异过大便会出现如图4-4右边所示的椭圆形等高线,具体分析将在4.2.3节中进行介绍。
在本节内容伊始,笔者便直接给出了梯度垂直于等高线的结论,下面先来大致分析一下梯度为什么会垂直于等高线。
设为平面上任意曲线,又由于曲线的法向量为。故,曲线的法向量为。可以发现,曲线也就是的法向量正好就是曲线对应的梯度,所以可以得出梯度垂直于曲线(等高线)的结论。
如图4-5所示,已知曲线,因此其在点的梯度。

又因为曲线在的斜率为
将代入得
所以曲线过点切线的一个方向向量为。
注:若直线斜率为,则他的一个方向向量为。
由此可得
所以有,即曲线在任意一点的梯度均垂直于曲线。因此,只有每次均沿着垂直于等高线的方向移动才能以最快的速度到达或远离原点,如图4-6所示。
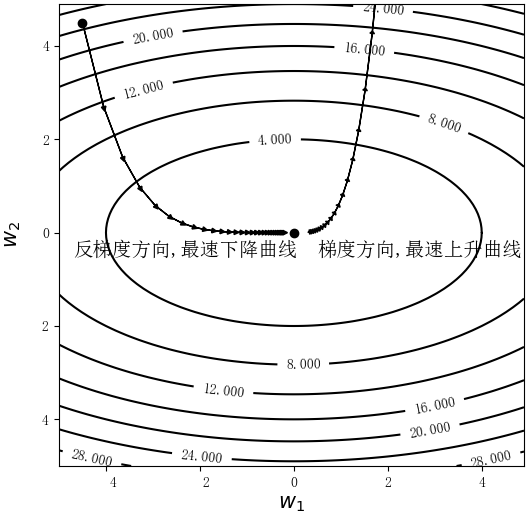
4.2.3标准化方法
1) 线性回归
以线性回归为例,假设某线性回归模型为,且,则此时便有如下目标函数(暂时忽略):
从式可以看出,由于,那么当产生相同的增量时,后者能产生更大的函数变化值,而这就引发了如图4-4右边所示“椭圆形”的环状等高线。
2) 逻辑回归
从上面的分析可以得知,在线性回归中若各个特征变量之间的取值范围差异较大,则会导致目标函数收敛速度慢等问题。换句话说哪怕是所有的特征变量取值都在类似的范围,便不会出现这类问题。那么在逻辑回归中又会有什么样的影响呢?由于在逻辑回归中,特征组合的加权和会作用上Sigmoid函数,所以影响目标函数收敛的除了上述因素外,更主要的还会取决于的大小。
如图4-7所示,黑色实线为的函数图像,黑色虚线为的函数图像。可以明显的看出,当或者左右时,,这也就意味着此时目标函数关于各个参数的梯度趋于0,从而使得参数在梯度下降过程中无法得到更新(或更新非常缓慢)。
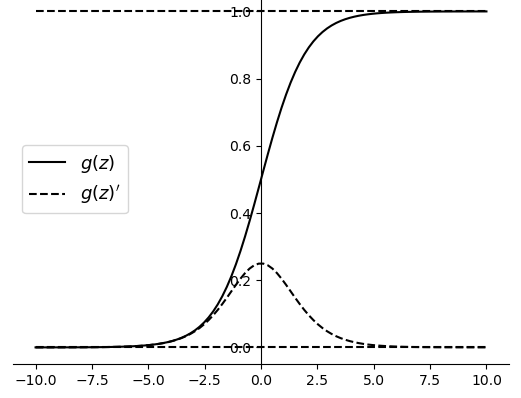
综上所述,在进行建模之前都应该对数据进行标准化。常见的标准化方法有很多种,这里暂时只介绍机器学习中应用最广泛的一种标准化方法,其标准化方式为
其中表示每一列特征的平均值,表示每一列特征的标准差。在进行标准化后,将使得每一列特征的均值都为0 ,方差都为1。其实现代码如下:
xxxxxxxxxx41def standarlization(X):2 mean = X.mean(axis=0)3 std = X.std(axis=0)4 return (X - mean) / std读者可自行通过提供的示例代码将特征标准化与未标准化后预测的结果进行一个对比,完整代码Chapter04/01_standarlization_reg.py文件。
4.2.4 特征组合与映射
在2.3.1节中介绍线性回归时,笔者通过一个预测梯形面积的示例来解释了特征组合的作用(丰富特征属性以提高预测精度)。但其实还可以从另外一个角度来理解特征组合。线性回归和逻辑回归从本质上讲都属于线性模型,因此对于基本的线性回归模型和逻辑回归模型来讲,其分别只能用于预测线性变化的实数和线性可分的类别,即对于如下图4-8所示的两种任务,两个基本模型均不能够完成。
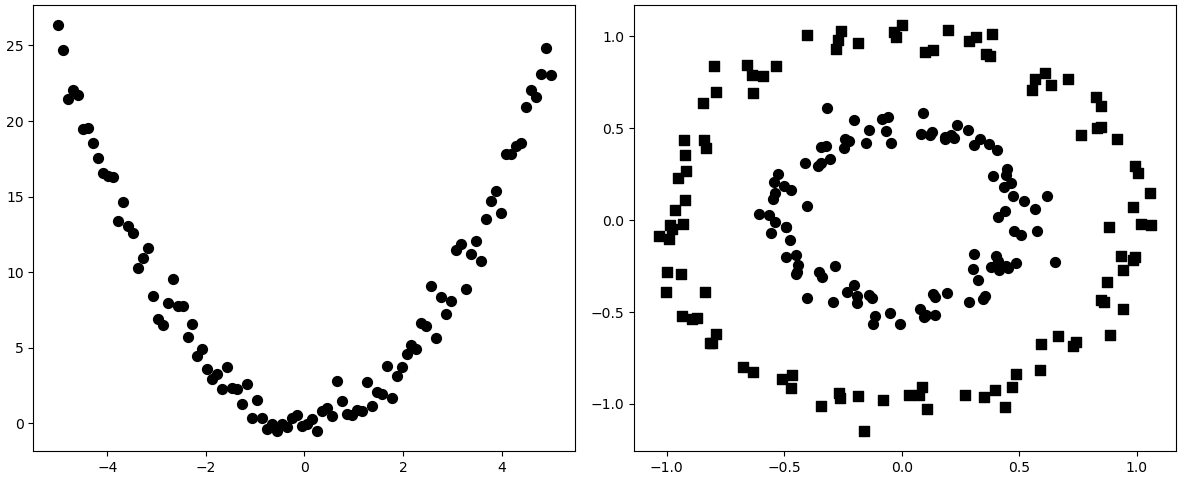
所谓特征映射是指将原来的特征属性通过某种方式,将其映射到高维空间的过程。当原有的特征被映射到高维空间后,就可能存在一个线性的超平面能够对数据进行很好的拟合[3]。因此,对于图4-8中所示的两种情形都可以通过2.3节介绍的方法将其映射为多项式特征后进行建模,如将映射为等等。但是对于上面的两个例子来说,只需要将原始特征映射至最高2次多项式就能完成相应的任务。
1) 非线性回归
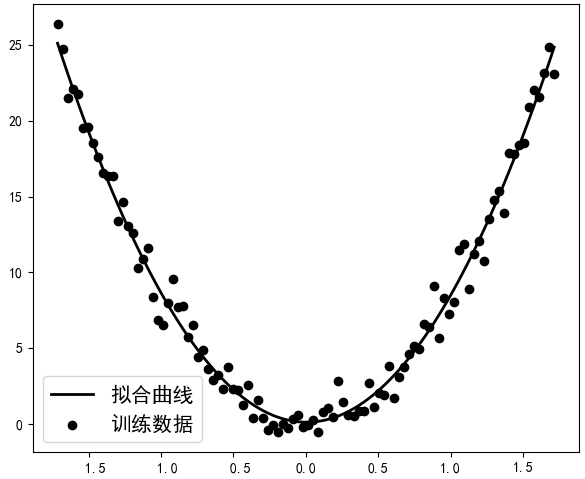
对于图4-8左边这个示例,首先需要构造一个模拟的数据集;然后再将整个特征维度映射为二次多项式;最后再进行回归即可拟合。完整代码见Chapter04/02_visualization_pol_reg.py文件。在拟合完成后便可以得到如图4-9所示的结果。
2) 非线性分类
对于图4-8右边的示例,首先同样需要构造一个模拟的数据集;然后再将整个特征维度映射为二次多项式;最后再进行拟合。完整代码见Chapter04/03_visualization_pol_cla.py文件。在拟合完成后便可以得到如图4-10所示的结果。

其中灰色与白色部分的交界处便是决策边界。
4.2.5 小结
在本节中,笔者先介绍了什么是等高线以及梯度与等高线之间的关系;然后介绍了为什么要对数据进行标准化以及一种常用的标准化方法;最后从另外一个角度介绍了特征组合与映射,以此来解决非线性的回归与分类问题。
4.3 过拟合
4.3.1 模型拟合
在上一节中,笔者介绍了为什么要对特征维度进行标准化,以及不进行标准化会带来什么样的后果。接下来,笔者就继续介绍其它的模型改善的方法和策略。
在2.5节内容中,笔者首次引入了梯度下降算法来最小化线性回归中的目标函数,并且在经过多次迭代后便可以求得到模型中对应的参数。此时可以发现,模型的参数是一步一步根据梯度下降算法更新而来直至目标函数收敛,也就是说这是一个循序渐进的过程。因此,这一过程也被称作是拟合(Fitting)模型参数的过程,当这个过程执行结束后就会产生多种拟合后的状态,例如过拟合(Overfitting)和欠拟合(Underfitting)等。
在线性回归中笔者介绍了几种评估回归模型常用的指标,但现在有一个问题是:当MAE或者RMSE越小就代表模型就越好吗?还是说在某种条件下其越小越好呢?细心的读者可能一眼便明了,肯定是有条件下的越小所对应的模型才越好。那这其中到底是怎么回事呢?
假设现在有一批样本点,它本是由函数生成(现实中并不知道),但由于其它因素的缘故,使得我们拿到的样本点并没有准确的落在曲线上,而是分布在其附近,如图4-10所示。

如图4-11所示,黑色圆点为训练集,黑色曲线为真实的分布曲线。现在需要根据训练集来建立并训练模型,然后得到相应的预测函数。假如分别用degree = 1,5,10来对这12个样本点进行建模(degree表示多项式的最高次数),那么便可以得到如图4-12所示的结果。
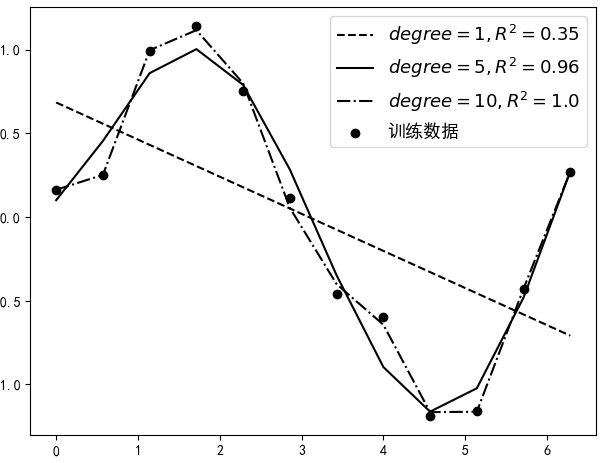
从图4-12中可以看出,随着多项式次数的增大,指标的值也越来越高(越大预示着模型越好),且当次数设置为10的时候,达到了1.0。但是最后就应该选degree=10对应的这个模型吗?
不知过了多久,突然一名客户来说要买你的这个模型进行商业使用,同时客户为了评估这个模型的效果自己又带来了一批新的含标签的数据(虽然这个模型已经用测试过,但客户并不会完全相信,万一你的这个模型作弊呢)。于是你拿着客户的新数据(也是由所生成),然后分别用上面的3个模型进行了预测,并得到了如图4-13所示的可视化结果。
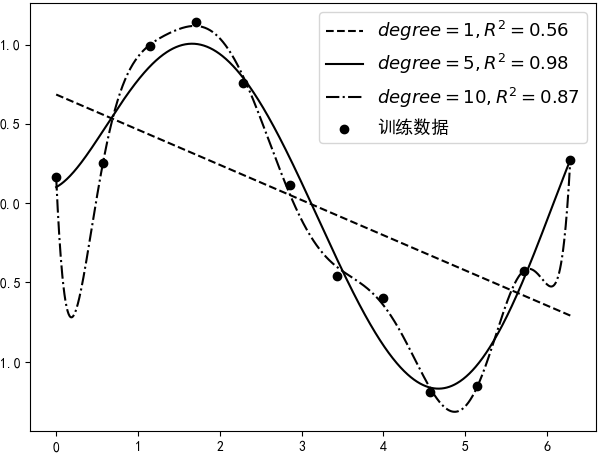
此时令你感到奇怪的是,为什么当degree=5时的结果居然会好于degree=10时模型的结果,问题出在哪儿?其原因在于,当第一次通过这12个样本点进行建模时,为了尽可能的使得“模型好(表现形式为尽可能大)”而使用了非常复杂的模型,尽管最后每个训练样本点都“准确无误”的落在了预测曲线上,但是这却导致最后模型在新数据上的预测结果严重的偏离了其真实值。
4.3.2 过拟合与欠拟合
在机器学习中,通常将建模时所使用的数据叫做训练集(Training Dataset),例如图4-11中的12个样本点;将测试时所使用的数据集叫做测试集(Testing Dataset)。同时把模型在训练集上产生的误差叫训练误差(Training Error);把模型在测试集上产生的误差叫泛化误差(Generalization Error);最后也将整个拟合模型的过程称作是训练(Training)[4]。
进一步,将4.3.1节中degree=10时所产生的现象叫做过拟合(Overfitting),即模型在训练集上的误差很小,但在测试集上的误差很大,也就是泛化能力弱;相反,将其对立面degree=1时所产生的现象叫做欠拟合(Underfitting),即模型训练集和测试集上的误差都很大;同时,将degree=5时的现象叫做恰拟合(Good Fitting),即模型在训练集和测试集上都有着不错的效果。
同时,需要说明的是,在4.3.1节中笔者仅仅是以多项式回归为例来向读者直观的介绍了什么是过拟合与欠拟合。但并不代表这种现象只出现在线性回归中,事实上所有的机器学习模型都会存在着这样的问题。因此一般来说,所谓过拟合现象指的就是模型在训练集上表现很好,而在测试集上表现糟糕;欠拟合现象是指模型在两者上的表现都十分糟糕;而恰拟合现象是指模型在训练集上表现良好(尽管可能不如过拟合时好),但同时在测试集上也有着不错的表现。
4.3.3 解决欠拟合与过拟合
1) 如何解决欠拟合
经过上面的描述我们已经对欠拟合有了一个直观的认识,所谓欠拟合就是训练出来的模型根本不能较好的拟合现有的训练数据。要解决欠拟合的方法相对来说较为简单,主要分为以下3种:
- 设计新的特征;收集或设计更多的特征维度作为模型的输入,即根据已有特征数据组合设计得到更多新的特征,这有点类似于上一点。
- 减小正则化系数;当模型出现欠拟合现象时,可以通过减小正则化中的惩罚系数来减缓欠拟合现象,这一点将在4.4节中进行介绍。
2) 如何解决过拟合
对于如何有效的缓解模型的过拟合现象,常见的做法主要分为如下4种:
- 收集更多数据;这是一个最为有效但实际操作起来又是最为困难的一个方法。训练数据越多,在训练过程中也就越能够纠正噪音数据对模型所造成的影响,使得模型不易过拟合。但是对于新数据的收集往往具有较大的困难。
- 降低模型复杂度;当训练数据过少时,使用较为复杂的模型极易产生过拟合现象,例如4.3.1中的示例。因此可以通过适当减少模型的复杂度来达到缓解模型过拟合的现象。
- 正则化方法;在出现过拟合现象的模型中加入正则化约束项,以此来降低模型过拟合的程度,这部分内容将在4.4节中进行介绍。
- 集成方法;将多个模型集成在一起,以此来达到缓解模型过拟合的目的,这部分内容将在第8章中进行介绍。
3) 如何避免过拟合
为了避免训练出来的模型产生过拟合现象,在模型训练之前一般会将拿到的数据集划分成两个部分,即训练集与测试集,且两者一般为7:3的比例。其中训练集用来训练模型(降低模型在训练集上的误差),然后用测试集来测试模型在未知数据上的泛化误差,观察是否产生了过拟合现象[3]。
但是由于一个完整的模型训练过程通常会是先用训练集训练模型,再用测试集测试模型。而绝大多数情况下不可能第一次就选择了合适的模型,所以又会重新设计模型(如调整多项式次数等)进行训练,然后再用测试集进行测试。因此在不知不觉中,测试集也被当成了训练集在使用。所以这里还有另外一种数据的划分方式,即训练集、验证集(Validation data)和测试集,且一般为7:2:1的比例,此时的测试集一般是通过训练集和验证集选定模型后做最后测试所用。
那实际训练中应该选择哪种划分方式呢?这一般取决于训练者对模型的要求程度。如果要求严苛那就划分为3份,如果不那么严格也可以划分为2份,也就是说这两者并没硬性的标准。
4.3.4小结
在这节中,笔者首先介绍了什么是拟合,进而介绍了拟合后带来的3种状态,即欠拟合、恰拟合与过拟合,其中恰拟合的模型是我们最终所需要的结果。同时,笔者接着介绍了解决欠拟合与过拟合的几种办法,其中解决过拟合的两种具体方法将在后续的内容中分别进行介绍。最后,笔者还介绍了两种方法来划分数据集来,以尽可能避免产生模型过拟合的现象。
4.4 正则化
从4.3节的内容可以知道,模型产生过拟合的现象表现为在训练集上误差较小,而在测试集上误差较大。并且笔者还说到,之所以产生过拟合现象是由于训练数据中可能存在一定的噪音,而我们在训练模型时为了尽可能的做到拟合每一个样本点(包括噪音),往往就会使用复杂的模型。最终使得训练出来的模型在很大程度上受到了噪音数据的影响,例如真实的样本数据可能更符合一条直线,但是由于个别噪音的影响使得训练出来的是一条弯曲的曲线,从而使得模型在测试集上表现糟糕。因此,可以将这一过程看作是由糟糕的训练集导致了糟糕的泛化误差。但仅仅从过拟合的表现形式来看糟糕的测试集(噪音多)也可能能导致糟糕的泛化误差。在接下来这节内容中,笔者将分别从这两个角度来介绍一下正则化(Regularization)方法中最常用的正则化是如何来解决这一问题的。
这里还是以线性回归为例,我们首先来看一下在线性回归的目标函数后面再加上一个正则化项的形式。
在式中的第2项便是新加入的正则化项(Regularization Term),那它有什么作用呢?根据2.1.3节中的内容可知,当真实值与预测值之间的误差越小(表现为损失值趋于),也就代表着模型的预测效果越好,并且可以通过最小化目标函数来达到这一目的。由式可知,为了最小化目标函数,第2项的结果也必将逐渐的趋于。这使得最终优化求解得到的均会趋于附近,进而得到一个平滑的预测模型。那这样做的好处是什么呢?
4.4.1 测试集导致糟糕的泛化误差
所谓测试集导致糟糕的泛化误差是指训练集本身没有多少噪音,但由于测试集含有大量噪音,使得训练出来的模型在测试集上没有足够的泛化能力,而产生了较大的误差。这种情况可以看作是模型过于准确而出现了过拟合现象。那正则化方法是怎么解决这个问题的呢?
假如式所代表的模型就是根据式中的目标函数训练而来,此时当新输入样本(含噪声)的某个特征维度由训练时的变成了现在的,那么其预测输出就由训练时的变成了现在的,即产生了的误差。但是,由于接近于附近,所以这使得模型最终只会产生很小的误差。同时,如果越接近于,那么产生的误差就会越小,这意味着模型越能够抵抗噪音的干扰,在一定程度提升了模型的泛化能力[5]。
由此便可以知道,通过在原始目标函数中加入正则化项,便能够使得训练得到的参数趋于平滑,进而能够使得模型对噪音数据不再那么敏感,缓解了模型过拟合的现象。
4.4.2 训练集导致糟糕的泛化误差
所谓糟糕的训练集导致糟糕的泛化误差是指,由于训练集中包含有部分噪音,导致我们在训练模型的过程中为了能够尽可能的最小化目标函数而使用了较为复杂的模型,使得最终得到模型并不能在测试集上有较好的泛化能力。但这种情况就完全是因为模型不合适而出现了过拟合的现象,而这也是最常见的过拟合原因。那正则化方法又是怎么解决在训练过程中就能够降低对噪音数据的敏感度的呢?为了便于后面理解,我们先从图像上来直观理解一下正则化到底对目标函数做了什么。
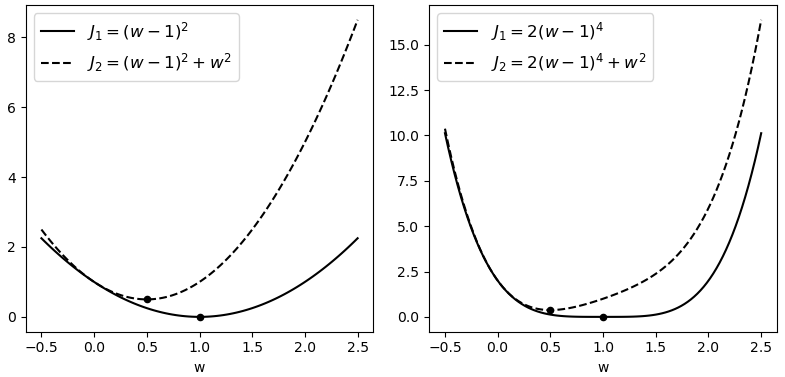
如图4-14所示,左右两边黑色实线为原始目标函数,黑色虚线为加了正则化后的目标函数。可以看出黑色实线的极值点均发生了明显的改变,且不约而同的都更靠近原点。
接下来再来看一张包含有两个参数的目标函数在加入正则化后的结果。
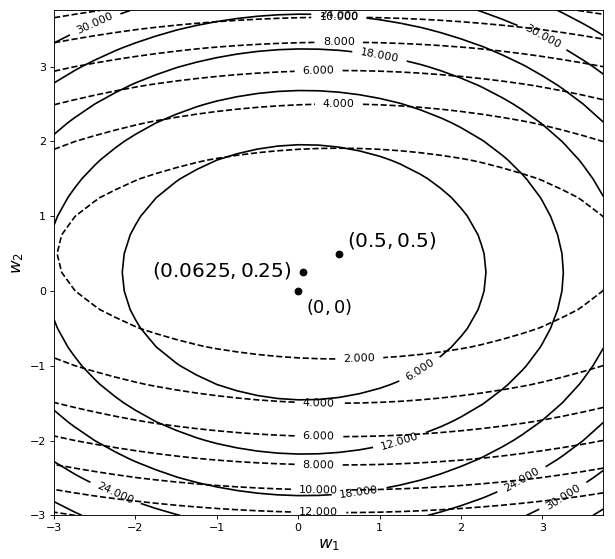
如图4-15所示,图中黑色虚线为原始目标函的等高线,黑色实线为施加正则化后目标函数的等高线。可以看出,目标函数的极值点同样也发生了变化,从原始的变成了,而且也更靠近原点(变得更小了)。到此我们似乎可以发现,正则化具有能够使得原始目标函数极值点发生改变,且同时还有使得参数趋于0的作用。事实上也正是因为这个原因才使得正则化具有缓解过拟合的作用,但原因在哪儿呢?
以目标函数为例,其取得极值的极值点为,且在极值点处的梯度为。当对其施加正则化后,由于的梯度方向是远离原点的(因为为一个二次曲面),所以给目标函数加入正则化,实际上就等价于给目标函数施加了一个远离原点的梯度。通俗点就是,正则化给原始目标函数的极值点施加了一个远离原点的梯度(甚至可以想象成是施加了一个力的作用)。因此,这也就意味着对于施加正则化后的目标函数来说,的极值点相较于的极值点更加的靠近于原点,而这也就是正则化本质之处。
假如有一个模型,它在含有噪音的训练集上表示异常出色,使得目标函数的损失值等于(也就是拟合到了每一个样本点),即在处取得了极值。现在,我们在 的基础上加入正则化项构成新的目标函数,然后再来分析一下通过最小化求得的模型到底产生了什么样的变化。
从式可知,由于是由加正则化项构成,同时根据先前的铺垫可知,将在离原点更近的极值点处取得的极值,即通过最小化含正则化项的目标函数,将得到这个最优解。但是请注意,此时的将不再是的最优解,即。因此通过最小化求得的最优解将使得,而这就意味着模型比模型更简单了,也就代表着从一定程度上缓解了的过拟合现象。
同时,由式可知,通过增大参数的取值可以对应增大正则化项对应的梯度,而这将使得最后求解得到更加简单的模型(参数值更加趋近于0)。也就是越大,一定程度上越能缓解模型的过拟合现象。因此,参数又叫做惩罚项(Penalty Term)或者惩罚系数。
最后,从上面的分析可知,在第一种情况中正则化可以看作是使得训练好的模型不再对噪音数据那么敏感;而对于第二种情况来说,正则化则可以看作是使得模型不再那么复杂。但其实两者的原理归结起来都是一回事,那就是通过较小的参数取值,使得模型变得更加简单。
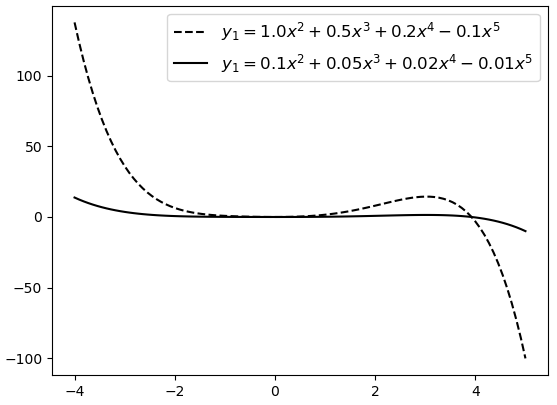
另外值得注意的一点是,很读者对于复杂模型存在着一个误解。认为高次数多项式表示的模型一定比低次数多项式表示的模型复杂,例如5次多项式就要比2次多项式复杂。但高次项代表的仅仅是更大的模型空间,其中既包含了复杂模型,也同时包含了简单模型。只需要将复杂模型对应位置的权重参数调整到更接近于0便可以对其进行简化。如图4-16所示,如果仅从幂次来看,两个模型一样“复杂”,但实际上虚线对应模型的复杂度要远大于实线对应模型的复杂度。
4.4.3 正则化中的参数更新
在给目标函数施加正则化后也就意味着其关于参数的梯度发生了变化。不过幸运的是正则化是被加在原有目标函数中,因此其关于参数的梯度也只需要加上惩罚项中对应参数的梯度即可,同时关于偏置的梯度并没有改变。下面笔者就总结一下线性回归和逻辑回归算法加上正则化后的变化。
1) 线性回归
可以发现,在梯度的求解公式中仅仅只是在的梯度后加入了新的一项。
2) 逻辑回归
从式可以看出,在逻辑回归的梯度求解公式中也仅仅只是在的后面加入了新的一项。同时可以发现,由于在施加了后,其目标函数关于的梯度增加的都是相同的部分。因此,此时的梯度下降公式为
从式可以看出,相较于之前的梯度下降更新公式,正则化会令权重先自身乘以小于1的系数,再减去不含惩罚项项的梯度。这将使得模型参数在迭代训练的过程中以更快的速度趋近于0,因此正则化又叫做权重衰减(Weight Decay)法[6]。
4.4.4 正则化示例代码
在介绍完正则化的原理后,下面以加入正则化的线性回归模型为例进行示例。完整代码见Chapter04/04_regularized_regression.py文件。
1) 制作数据集
由于这里要模拟模型的过拟合现象,所以需要先制作一个容易导致过拟合的数据集,例如特征数量远大于训练样本数量。具体代码如下:
xxxxxxxxxx71def make_data():2 n_train, n_test, n_features = 50, 100, 1003 w, b = np.ones((n_features, 1)) * 0.2, 2 4 x =np.random.normal(size=(n_train + n_test, n_features))# 5 y = np.matmul(x, w) + b #用来生成正确标签6 y += np.random.normal(scale=0.2, size=y.shape)7 return x,u在上述代码中,第3行用来初始化权重和偏置;第5-6行用来随机生成样本的输入特征,同时再加上相应的噪音。
2) 定义目标函数
为了后续方便观察模型的收敛情况,需要定义包含正则化项的目标函数,代码如下:
xxxxxxxxxx61def cost_function(X, y, W, bias, lam):2 m, n = X.shape3 y_hat = prediction(X, W, bias)4 J = 0.5 * (1 / m) * np.sum((y - y_hat) ** 2) 5 Reg = lam / (2 * n) * np.sum(W ** 2) #正则化项6 return J + Reg在上述代码中,第4行就是普通线性回归中的目标函数;第5行表示正则化项;最后再返回原始目标函数加上正则化项的结果。
3) 定义梯度下降
加入正则化后,只需要在参数的梯度后加上对应正则化方法的梯度即可,代码如下:
xxxxxxxxxx81def gradient_descent(X, y, W, bias, alpha, lam):2 m, n = X.shape3 y_hat = prediction(X, W, bias)4 grad_w = -(1 / m) * np.matmul(X.T, (y - y_hat)) + (lam / n) * W 5 grad_b = -(1 / m) * np.sum(y - y_hat) 6 W = W - alpha * grad_w 7 bias = bias - alpha * grad_b8 return W, bias整体上与2.7.4节中定义的梯度下降代码一样,仅仅只是在普通线性回归梯度的最后加上了正则化项对应的梯度。
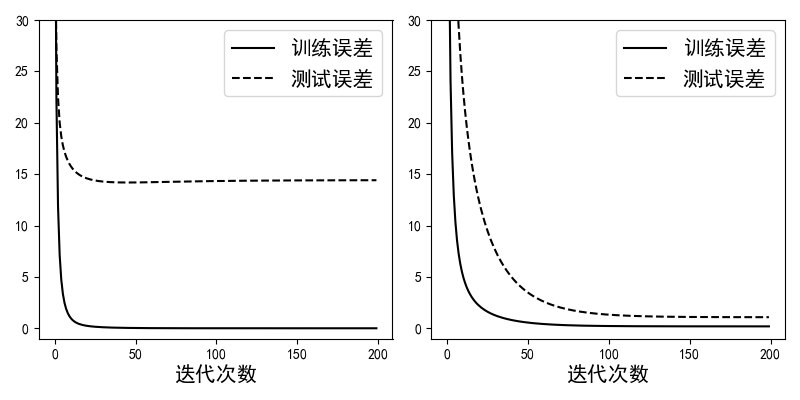
在定义完上述各个函数后,便可以用来训练带正则化项和不带正则化项(lam参数设为0)的线性回归模型。如图4-17所示,左边为未添加正则化项时训练误差和测试误差的走势。可以明显看出模型在测试集上的误差远大于在训练集上的误差,这就是典型的过拟合现象。右图为使用正则化后模型的训练误差和测试误差,可以看出虽然训练误差有些许增加,但是测试误差得到了很大程度上的降低[6]。这就说明正则化能够很好的缓解模型的过拟合现象。
4.4.5 小结
在这节内容中,笔者首先通过示例详细介绍了如何通过正则化方法来缓解模型的过拟合现象,以及介绍了为什么正则能够使模型变得更简单;其次笔者介绍了加入正则化后原有梯度更新公式的变化之处,其仅仅只是加上了正则化项对应的梯度;最后笔者通过一个示例来展示了正则化的效果。但与此同时,这里笔者只是介绍了使用最为频繁的正则化,例如还有正则化等,读者可以自行查阅。
4.5 偏差方差与交叉验证
在第4.4节中,笔者介绍了什么是正则化,以及正则化为什么能够缓解过拟合的原理。同时我们可以知道,越是复杂的模型越是可能产生过拟合的现象,这也就为模型在其它未知数据集上的预测带来了误差。但是这些误差来自哪里,是怎么产生的呢?知道这些误差的来源后对改善我们的模型有什么样的帮助呢?接下来笔者就来介绍关于误差分析以及模型选择的若干方法。
4.5.1 偏差与方差定义
在机器学习的建模中,模型普遍的误差都是来自于偏差(Bias)或方差(Variance)。那什么又是偏差与方差呢?
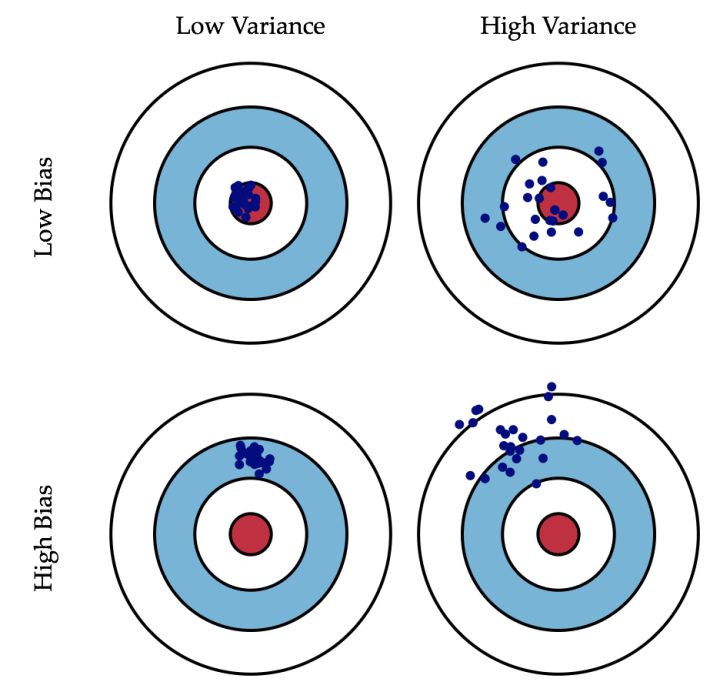
如图4-18所示[7],假设你拿着一把枪打击红色的靶心,在你连打数十枪后出现了以下四种情况:
- 所有子弹都密集打在靶心旁边的位置,这就是典型的方差小(子弹很集中),偏差大(距离靶心甚远);
- 子弹都散落在靶心周围的位置,这就是典型的方差大(子弹很散乱),偏差小(都在靶心附近);
- 子弹都散落在靶心旁边的位置,这就是典型的方差大(子弹散乱),偏差大(距离靶心甚远);
- 所有子弹都密集打在了红色靶心的位置,这就是典型的方差小(子弹集中),偏差小(都在靶心位置);
由此可知,偏差描述的是预测值的期望与真实值之间的差距,即偏差越大,越偏离真实值,如图4-18第2行所示。方差描述的是预测值之间的变化范围(离散程度),也就是离其期望值的距离。即方差越大,数据的分布越分散,如图4-18右列所示。
4.5.2 模型的偏差与方差
上面介绍了什么是偏差与方差,那么这4种情况又对应机器学习中的哪些场景呢?通常来说,一个简单的模型会带来比较小的方差(Low Variance),而复杂的模型会带来比较大的方差(High Variance)。这是由于简单的模型不容易受到噪音的影响,而复杂的模型(例如过拟合)容易受到噪音的影响而产生较大的误差。一个极端的例子,这个模型不管输入是什么,输出都是常数,那么其对应的方差就会是0。对于偏差来说,一个简单的模型容易产生较高偏差(High Bias),而复杂的模型容易产生较低的偏差(Low Bias),这是由于越复杂的模型越容易拟合更多的样本。
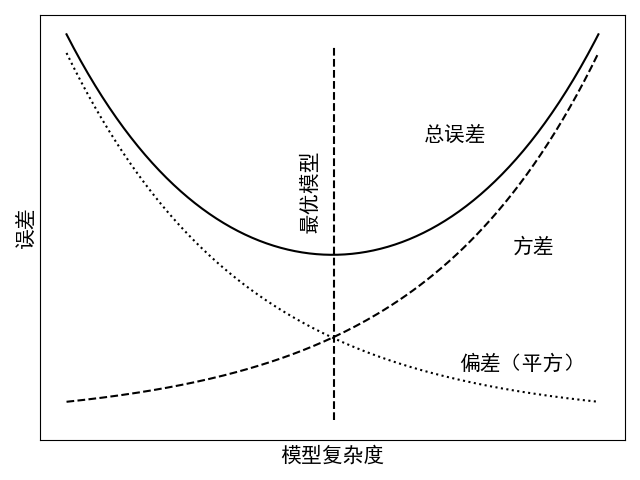
如图4-19所示为模型的偏差、方差与模型复杂度的变化情况。从图中可以看出,方差随着模型的复杂度增大而上升,偏差与之恰好相反。同时,如果一个模型的主要误差来自于较大的方差,那么这个模型呈现出的就是过拟合的现象;而一个模型的主要误差来自于较大的偏差时,那么此时模型呈现出的就是欠拟合现象。
总结就是,模型的高方差与高偏差分别对应过拟合与欠拟合。如果一个模型不能很好的拟合训练样本,那么此时模型呈现的就是高偏差(欠拟合)的状态;如果是能够很好的拟合训练样本,但是在测试集上有较大的误差,这就意味着此时模型出现了高方差(过拟合)的状态。因此,当模型出现这类情况时,我们完全可以按照前面处理过拟合与欠拟合的方法对模型进行改善,然后在这两者之间进行平衡。
4.5.3 超参数选择
在之前的介绍中,我们知道了模型中的权重参数可以通过训练集利用梯度下降算法求解得到,但超参数又是什么呢?所谓超参数(Hyper Parameter)是指那些不能通过数据集训练得到的参数,但它的取值同样会影响到最终模型的效果,因此同样重要。到目前为止,我们一共接触过了3个超参数,只是第一次出现的时候笔者并没有可以提起其名字,在这里再做一个细致的总结。这三个超参数分别是:惩罚系数,学习率、以及特征映射时多项式的次数,其中最为重要的就是前面两个。
1) 惩罚系数
从4.4节内容中对正则化的介绍中可知,越大也就意味着对模型的惩罚力度越大,最终训练得到的模型也就相对越简单。因此,在模型的训练过程中,也需要选择一个合适的来使得模型的泛化能力尽可能好。
2) 学习率
在介绍线性回归的求解过程中,笔者首次介绍了梯度下降算法,如式所示。
并且说到,的作用是用来控制每次向前跳跃的距离,较大的可以更快的跳到谷底找到最优解。但是过大的同样能使得目标函数在峡谷的两边来回振荡,以至于需要多次迭代才能得到最优解(甚至可能得不到最优解)。
如图4-20所示为相同模型采用不同学习率后,经梯度下降算法在同一初始位置优化后的结果,其中黑色五角星表示全局最优解(Global Optimum),表示迭代次数。
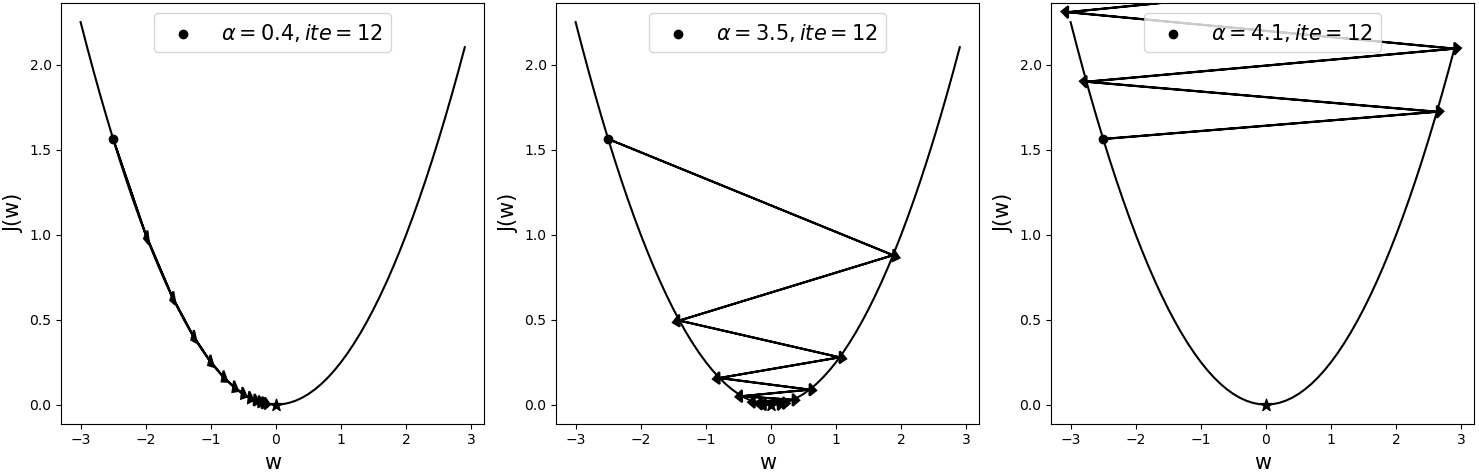
从图4-20可以看出,当学习率为0.4时,模型大概在迭代12次后就基本达到了全局最优解。当学习率为3.5时,模型在大约迭代12次后同样能够收敛于全局最优解附近。但是,当学习率为4.1时,此时的模型已经处于了发散状态。可以发现,由于模型的目标函数为凸函数(例如线性回归),所以尽管使用了较大的学习率3.5,目标函数依旧能够收敛。但在后面的学习过程中,遇到更多的情况便是非凸型的目标函数,此时的模型对于学习率的大小将会更加敏感。
如图4-21所示为一个非凸型的目标函数,三者均从同一初始点开始进行迭代优化,只是各自采用了不同的学习率。其中黑色五角星表示全局最优解,表示迭代次数。
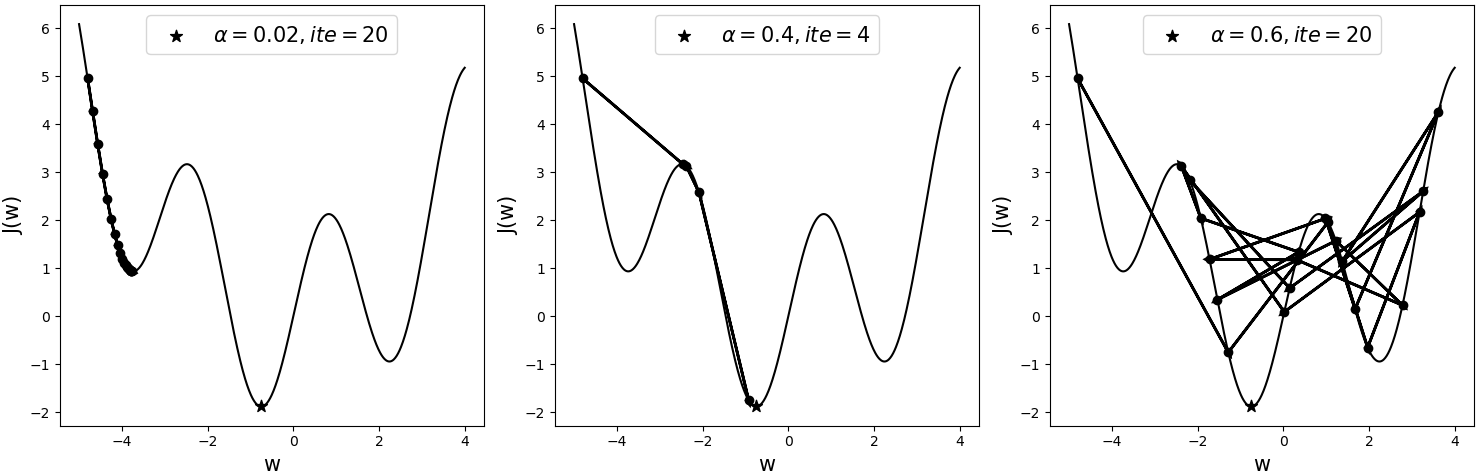
从图4-21可以看出,当采用较小的学习率0.02时,模型在迭代20次后陷入了局部最优解(Local Optimum);并且可以知道此时无论再继续迭代多少次,其依旧会收敛于此处,因为它的梯度已经开始接近于0,而使得参数无法得到更新。当采用较大一点的学习率0.4时,模型在迭代4次后便能收敛于全局最优解附近。当采用学习率为0.6时,模型在这20次的迭代过程中总是来回振荡,并且没有一次接近于全局最优解。
从上面两个示例的分析可以得出,学习率的大小对于模型的收敛性以及收敛速度有着严重的影响,且非凸函数在优化过程中对于学习率的敏感性更大。同时值得注意的是,所谓学习率过大或者过小,在不同模型间没有可比性。例如在上面凸函数的图示中学习率为0.4时可能还算小,但是在非凸函数的这个例子中0.4已经算是相对较大了。
经过上面的介绍,我们明白了超参数对于模型最终的性能有着重要的影响。那到底应该如何选择这些超参数呢?对于超参数的选择,首先可以先列出各个参数的备选取值,例如,;然后再根据不同的超参数组合训练得到不同的模型(比如这里就有25个备选模型),然后再通过4.5.4节介绍的交叉验证来确立模型。不过这一整套的步骤sklearn也有现成的类方法可以使用,并且使用起来也非常方便,在4.6中将会通过一个详细的示例进行说明。不过随着介绍的模型越来越复杂,就会出现更多的超参数组合,训练一个模型也会花费一定的时间。因此,对于模型调参的一个基础就是要理解各个参数的含义,这样才可能更快的排除不可能的参数取值,以便于更快的训练出可用的模型。
4.5.4 模型选择
当在对模型进行改善时,自然而然的就会出现很多备选模型。而我们的目的便是尽可能的选择一个较好的模型,以达到低偏差与低方差之间的平衡。那该如何选择一个好的模型呢?通常来说有两种方式:第一种就是4.3.3节中介绍过的将整个数据集划分成3部分的方式;第二种则是使用K折交叉验证(K-fold Cross Validation)[5]的方式。对于第一种方法,其步骤为先在训练集上训练不同的模型,然后在验证集上选择其中表现最好的模型,最后在测试集上测试模型的泛化能力。但是这种做法的缺点在于,对于数据集的划分可能恰好某一次划分出来的测试集含有比较怪异的数据,导致模型表现出来的泛化误差也很糟糕。那么此时就可以通过K折交叉验证来解决。
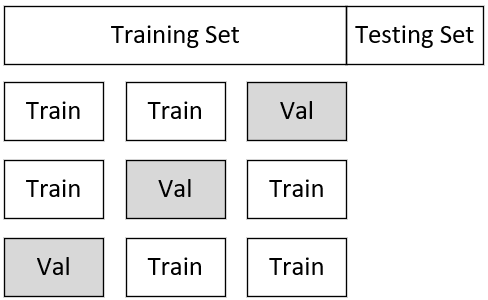
如图4-22所示,以3折交叉验证为例,首先需要将整个完整的数据集分为训练集与测试集两个部分。并且同时再将训练集划分成3份,每次选择其中两份作为训练数据,另外一份作为验证数据进行模型的训练与验证,最后再选择平均误差最小的模型。
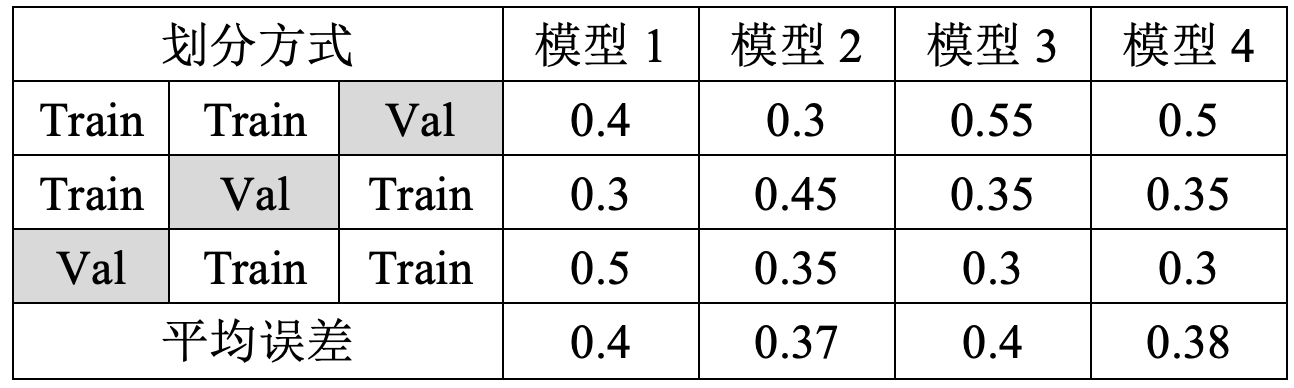
假设现在有4个不同的备选模型,其各自在不同验证集上的误差如表4-1所示。根据得到的结果,可以选择平均误差最小的模型2作为最终选择的模型。然后再将其用整个大的训练集训练一次,最后用测试集测试其泛化误差。当然,还有一种省略的交叉验证方式,即一开始并不再划分出测试集,而是直接将整个数据划分成为K份进行交叉验证,然后选择平均误差最小的模型即可。整个详细的示例过程将在4.6节内容中进行介绍。
4.5.5 小结
在这节内容中,笔者首先通过一个例子直观地介绍了什么是偏差与方差,以及在机器学习中当模型出现高偏差与高方差时所对应的现象和处理方法;然后介绍了什么是超参数以及超参数能够给模型带来什么样的影响;最后介绍了在改善模型的过程中如何通过K折交叉验证来进行模型的选择。在4.6节内容中,笔者将通过一个真实的例子来对上述过程进行完整的介绍。
4.6 实例分析手写体识别
经过前面几节的介绍,我们对模型的改善与泛化已经有了一定的认识。下面笔者就通过一个实际的手写体分类任务进行示范,介绍一下常见的操作流程。同时顺便介绍一下sklearn和matplotlib中常见方法的使用,完整代码见Chapter04/05_digits_classification.py文件。
4.6.1 数据预处理
在4.2.3节中,笔者详细介绍了为何需要对输入特征进行标准化操作,以及一种常见的标准化方法。接下来,就来看一下标准化在模型训练过程中的具体流程。
1) 载入数据集
首先,需要载入训练模型时所用到的数据集。这里以sklearn中常见的手写体数据集load_digits为例,代码如下:
xxxxxxxxxx41def load_data():2 data = load_digits()3 x, y = data.data, data.target4 return x,yload_digits数据集一共包含有1797个样本10个类别,每个样本包含有64个特征维度。在载入完成后还可以对其进行可视化,如图4-23所示。

2) 划分数据集
其次,在开始进行标准化之前,需要将数据集分割成训练集和测试集两个部分,这里可以借助sklearn中的train_test_split方法来完成,代码如下:
xxxxxxxxxx51from sklearn.model_selection import train_test_split2def load_data():3 #此处接“1.载入数据集”中代码4 x_train, x_test, y_train, y_test = \5 train_test_split(x, y, test_size=0.3, random_state=20)在上述代码中,第5行里test_size=0.3表示测试集的比例为30%,random_state=20表示设置一个状态值,它的作用是使得每次划分的结果都是一样的,同时也可以设置其它值。同时,在sklearn中对于包含随机操作的函数或者方法,一般都有这个参数,固定下来的目的是便于其他人复现你的结果。
3) 对训练集标准化
然后,对训练集进行标准化,并保存标准化过程中计算得到的相关参数。例如以4.2.3节中的方法进行标准化时,就需要保存每个维度对应的均值和标准差。这里以可以借助sklearn中的StandardScaler方法来完成,代码如下:
xxxxxxxxxx51from sklearn.preprocessing import StandardScaler2def load_data():3 #此处接“2.划分数据集”中代码4 ss = StandardScaler()5 x_train = ss.fit_transform(x_train)在上述代码中,第4行用来定义4.2.3节中的标准化方法;第5行先计算每个维度需要用到的均值和方差,然后再对每个维度进行标准化;同时,第5行也可以分开来写,如下:
xxxxxxxxxx51def load_data():2 #此处接“2.划分数据集”中代码3 ss = StandardScaler()4 ss.fit(x_train) #先计算每3个维度需要用到的均值和方差 5 x_train = ss.transform(x_train)#再对每个维度进行标准化4) 对测试集标准化
最后,利用在训练集上计算得到的参数,对测试集(以及未来的新数据)进行标准化,代码如下:
xxxxxxxxxx31def load_data():2 #此处接“3.对训练集标准化”中代码3 x_test = ss.transform(x_test)这里只能使用.transform()方法来对测试集进行标准化,因为在第2步中已经在训练集上得到了标准化所需要用到的参数(均值和方差)。如果这里再使用.fit_transform()方法来进行标准化,那么便是根据测试集中的参数来对测试集进行标准化,而这将严重影响模型在未来新数据上的泛化能力。
注意:无论用什么方法对数据集进行标准化,都必需要遵循上述的4个步骤。
4.6.2 模型选择
正如4.5节中的介绍,不同的模型实际上是根据选择不同的超参数所形成的。因此,选择模型的第一步就是确定好有哪些可供选择的超参数,以及每个超参数可能的取值。由于此处将采用逻辑回归算法对图片进行分类,所以目前涉及到的超参数仅有学习率和惩罚系数。下面,就根据4.5节中介绍的方法来一步步完成模型的选择过程。
1) 列举超参数
根据分析,这里需要列出学习率和惩罚系数的可能取值,代码如下:
xxxxxxxxxx21learning_rates = [0.001, 0.03, 0.01, 0.03, 0.1, 0.3, 1, 3]2penalties = [0, 0.01, 0.03, 0.1, 0.3, 1, 3]在这里,取值方法一般来说可以每次扩大3倍,但是也可以每次都增加相同的步长(例如0.002),只不过这需要花费更多的时间来遍历完所有可能的超参数组合,具体可以视情况而定。
2) 定义模型
在列举出所有参数的可能取值后,就需要遍历所有的参数组合,代码如下:
xxxxxxxxxx61from sklearn.linear_model import SGDClassifier2for learning_rate in learning_rates:3 for penalty in penalties:4 print(f"训练模型:learning_rate={learning_rate}, penalty={penalty}")5 model = SGDClassifier(loss='log', penalty='l2', learning_rate = 'constant', 6 eta0=learning_rate, alpha=penalty)在上述代码中,第5行使用的是sklearn中的SGDClassifier类来建立逻辑回归模型。它与第3章中介绍的LogisticRegression的区别在于,前者并没有通过梯度下降来进行参数求解,而后者使用的便是梯度下降算法进行求解。同时,在SGDClassifier中可以通过loss='log'来指定为逻辑回归;通过penalty='l2'来指定为正则化;通过learning_rate='constant'来指定使用自定义的学习率,即根据eta0=learning_rate来设定,因为默认SGDClassifier中的学习率都是根据训练过程动态适应的;通过alpha=penalty来指定相应的惩罚系数。
3) 交叉验证
根据不同的超参数组合定义得到不同的模型后,就需要对训练集进行划分以实现模型的交叉验证。在这里可以借助sklearn中的KFold方法来对训练集进行划分,代码如下:
xxxxxxxxxx81from sklearn.model_selection import KFold2model = ……此处接“2.定义模型”中代码3kf = KFold(n_splits=k, shuffle=True, random_state=10)4for train_index, dev_index in kf.split(X):5 X_train, X_dev = X[train_index], X[dev_index]6 y_train, y_dev = y[train_index], y[dev_index]7 model.fit(X_train, y_train)8 s = model.score(X_dev, y_dev)在上述代码中,第3行用来生成交叉验证时样本对应的索引,其中n_splits=k表示使用k折交叉验证,shuffle=True表示在划分时对训练集进行随机打乱;第4行用来取每一次交叉验证时样本的索引,即根据这些索引来获取每次对应的训练集和验证集。最后再调用模型中的.fit()方法来进行训练。
当执行完上述代码后,便能够得到如下所示的运行结果:
xxxxxxxxxx51正在训练模型: learning_rate = 0.001, penalty = 02正在训练模型: learning_rate = 0.001, penalty = 0.013……4正在训练模型: learning_rate = 3, penalty = 35最优模型: [0.9554322392967812, 0.03, 0]经过交叉验证的选择后可以发现,当学习率为0.03,惩罚系数为0时对应的模型为最优模型。同时,由于备选的学习率有8个,备选的惩罚系数有7个,并且这里采用了5折交叉验证,因此一共就需要拟合280次模型。
4.6.3 模型测试
通过交叉验证选择完模型后,就可以再用完整的训练集对该模型进行训练,然后在测试集上测试其泛化误差,代码如下:
xxxxxxxxxx41model = SGDClassifier(loss='log', penalty='l2', learning_rate='constant', eta0=0.03, alpha=0.0)2model.fit(x_train, y_train)3y_pred = model.predict(x_test)4print(classification_report(y_test, y_pred))在运行完上述代码后,便能够得到如下结果:
xxxxxxxxxx41 precision recall f1-score support2 accuracy 0.96 5403 macro avg 0.96 0.96 0.96 5404weighted avg 0.96 0.96 0.96 540到此,对于一个模型从数据预处理到模型选择,再到模型测试的全部流程就介绍完了。不过上述过程在模型选择部分需要自己来手动划分数据集进行交叉验证选择模型,这样看起来稍微有点繁琐。不过好在sklearn已经将上述过程进行了封装,只需要几行代码就能实现上述完整过程。这部分内容将在第5章中进行介绍。
4.6.4 小结
在本节中,笔者首先通过逻辑回归算法进行了手写体分类的示例,介绍了如何对数据集进行预处理以及其对应的完整流程;接着介绍了如何对备选模型进行选择,包括列举超参数、定义模型以及进行交叉验证等步骤;最后介绍了如何测试最优模型的泛化误差。
总结一下,在本章中笔者首先介绍了什么是特征标准化、为什么需要特征标准化以及一种常见的特征标准化方法;接着介绍了什么是过拟合与欠拟合、如何通过正则化方法来缓解模型的过拟合现象以及正则化背后的原理;然后介绍了什么是模型的偏差与方差以及模型如何对模型进行选择的方法;最后通过一个完整的手写体识别示例展示了从数据预处理(包括载入数据、划分数据和标准化数据)到模型选择(包括列举模型参数、定义模型和交叉验证),再到模型测试的完整流程。对于这部分内容的介绍就暂时先告一段落。不过在后续章节的介绍中,笔者也会继续补充相关提高模型性能的方法与技巧。
本次内容就到此结束,感谢您的阅读!如果你觉得上述内容对你有所帮助,欢迎分享至一位你的朋友!若有任何疑问与建议,请添加笔者微信'nulls8'或加群进行交流。青山不改,绿水长流,我们月来客栈见!
引用
[1]https://en.wikipedia.org/wiki/Machine_learning
[2]The Discipline of Machine Learning, Tom M. Mitchell, July 2006 CMU-ML-06-108
[3]Andrew Ng, Machine Learning, Stanford University, CS229, Spring 2019.
[4]Ian,Goodfellow, et al. Deep Learning. 深度学习 中文译本 人民邮电出版社
[5]Hung-yi Lee, Machine Learning, National Taiwan University, 2020, Spring.
[6]李沐, 动手学深度学习, 人民邮电出版社
[7]图片来自:http://scott.fortmann-roe.com/docs/BiasVariance.html


